Two commercial applications of a chosen nonlinear optical material
Table of Contents
| Introduction: |
| Parametric amplifiers |
| Waveguides |
| The Pockels effect waveguides |
| Second Harmonic Generation waveguides |
| Conclusion |
| References |
A nonlinear optical material is one in which the interaction of the electromagnetic field of light and the electric field of the optical material is not proportional to the induced polarization (Schawlow, 1969; Parker, 1989).
In an optical material, when an alternating electric field of visible light wave is incidented onto a surface, the heavy nuclei and tightly bound inner electrons of the atoms cannot respond to the rapid changes in the alternating field (Giordmaine, 1964). However, the loosely bound valence electrons are able to follow the pattern of the field and redistributes itself according to this pattern, thereby causing a periodical changing polarization (Giordmaine, 1964). The negative charge density inside the atom corresponds to the oscillating polarization, and thus a weak alternating current is induced at the light frequency (Fig 1) (Girodmaine, 1964). This is a linear optical behaviour and is exhibited by all optical materials (Giordmaine, 1964). If on the other hand an intense light like an laser with a large electric field, about 107 volts/cm was incidented onto an optical material, a massive distribution of charge occurs or large induced polarization, since the electric field is comparable in size to that of the cohesive local electric fields of the material (108 to 1010 volts/cm) (Giordmaine, 1964). The polarization is thus not proportional to the optical electric field an this is a nonlinear optical behaviour (Fig 2) (Giordmaine, 1964). The polarization wave produced in an noncentrosymmetric material has three components:
a) a wave at the fundamental frequency of the light wave (w )
b) a wave at the second-harmonic frequency (2w )
c) a 'direct current' or steady polarization (Fig 3) (Bowden, 1988; Roberts, 1988; Williams, 1988).
In centrosymmetric materials the same components are found except a wave at the third harmonic frequency is produced (3w ) (Bowden, 1988; Roberts, 1988; Williams, 1988).
. The overall polarization experienced in the material may be written as:
P = c (1) E + c (2)E2 + c (3)E3....... (1)
where
P is the macroscopic polarization
E is the local coherent electric field due to the radiation
c (1), c (2) and c (3) are second, third and fourth rank susceptibility tensors (Bowden, 1988; Roberts, 1988; Williams, 1988).
The optical nonlinear material understudy in this paper is Gallium arsenide (GaAs). This material is used in many semiconductor devices, but not usually for its nonlinear properties. This paper will discuss only the nonlinear properties associated with c (2) in GaAs and how it is use in integrated optics for communication industry. GaAs has a particularly large c (2) about 10-7 esu (Williams, 1988), and low birefringence which gives a good condition for nonlinear interactions (Anderson and Boyd, 1971). There are three main effects than can be observed for c (2) which are:
1) Frequency mixing
2) Second harmonic generation
3) Producing the linear electrooptic or Pockels effect (Williams, 1988).
In this paper, the all three effects would be taken into consideration and would be applied to the nonlinear GaAs crystal.
The parametric amplifiers use the effect of frequency mixing (Williams, 1988). If the incidented light source have different electric fields w a and w b, the beat frequencies will occur in the polarization at w a ± w b (Williams, 1988). The electric field distributions produced are determined by the magnitude of the nonlinear coefficient c (2), the path length in which the interaction occurs, and the phases of the wave (Williams, 1988). In the case of frequency difference mixing w a - w b, if w a is the more intense 'pump' wave and w b is the weak 'idler' wave, the nonlinear interaction will leads to the splitting of w a into two lower frequency photons and the amplification of w b, (Williams, 1988).
The amplification takes place in the varactor diodes or variable reactor diodes which are connected to the light source (Hyde, 1965). It behaves as a low-loss nonlinear 'capacitor' over a wide range of forward and reverse bias voltages from the light (Hyde, 1965). The diode is made up of a p-n junction of moveable plates of GaAs (Hemmenway et al, 1967). The 'capacitor' behaviour is achieved when the potential difference is changed between the p and n sides (Hemmenway et al, 1967). The charges moving across from both sides form a depletion layer where the charges are stored (Fig. 4) (Hemmenway et al, 1967). The depletion layer with the stored charge unlike in the capacitor is not proportional to the potential difference (Hemmenway et al, 1967). When the voltage is at a peak the plates are pulled apart quickly (Hemmenway et al, 1967). After separation the capacitance is very small but the charge remains the same since the time taken for the separation is small compared to that of the resonant circuit (Hemmenway et al, 1967). The peak voltage corresponds to the maximum electric force acting to pull the plates together (Giordmaine, 1964). The increased voltage remains across the capacitor in its cycle and returns to zero, when the electric force is zero, the plates at this point are pushed back into their original position (Giordmaine, 1964; Hemmenway et al, 1967). The mechanical work thus goes into amplifying the incoming voltage wave, w b (Giordmaine, 1964; Hemmenway et al, 1967). This 'pumping' effect of the plates are due to the pump signal, w a, usually a laser source (Fig 5) (Giordmaine, 1964; Hemmenway et al, 1967). In order for maximum energy to be transferred, the capacitance must be varied in proper phase at exactly twice the signal frequency that is at 2w a (Hemenway et al, 1967, Giordmaine, 1964).
Gallium arsenide is used particularly in these cases since its electron mobility is higher than its other counterparts, silicon and germanium, and thus has a higher conductivity in the n-base type material (Hyde, 1965). The varactor diodes in parametric amplifiers generate very little spurious noise and are used mainly in earth stations of optical communication systems, that is for amplifying the signals of the microwaves and for detecting repeaters, (Brown, 1978; Williams, 1988). The parametric amplification is also extremely useful in spectroscopy for detecting weak signals and producing sufficient coherent far infrared light to be used in other associated spectroscopic related work (Giordmaine, 1964; Williams 1988). The infrared light produced by lasers (40% efficiency) in the parametric amplifiers may be also used in pilot lights, optical-electronic data, ranging systems and direct sight communication as in infrared lamps for height division devices and alphanumeric data displays (Fischer, 1978).
Waveguides are materials that allow electromagnetic radiation to be channelled or 'filtered out' into their respective components (Lindsay, 1978). These thin films waveguides are used in integrated optical circuitry (Tien, 1971). However, waveguides are not restricted to being made by nonlinear materials. The optical nonlinear waveguides may make use of the effect of SHG (Williams, 1988) or the Pockels effect (Bowden, 1988).
The linear electrooptic or Pockels effect arises when the polarization components from the interaction of the light optical field propagating in the nonlinear medium, E(w) and the direct current, E(0) or the field applied to the electrode alters the propagation characteristics of light in the medium (Bowden,1988; Williams, 1988). The propagation characteristics are described by an ellipsoid with component along the principal dielectric axes 1/nx2, 1/ny2 and 1/nz2 (Bowden,1988; Williams, 1988). The changing of these values by applying an electric field are dependent upon the symmetry of the medium (Bowden,1988; Williams, 1988). The effects that may achieved from the changing of these values are rotate polarization, frequency or amplitude modulation or diffraction of light if there is a periodic index modulation (Bowden,1988; Williams, 1988). The values for the diffraction of light are used in the waveguides (Bowden,1988; Williams, 1988). These waveguides are used for mainly for multiplexers, a device for separating different wavelengths of light, (Bowden,1988; Williams, 1988). GaAs may be used in these waveguides but it has a low electrooptic coefficient and materials such as Lithium niobate is more suitable (Bowden,1988; Williams, 1988).
Second Harmonic Generation waveguides
Second harmonic generation, SHG, is the combination of two photons at a frequency w to produce a new photon at 2w (Williams, 1988). The nonlinear polarization which is created in the waveguide medium contains a Fourier component at 2w which acts as a source of electromagnetic radiation at 2w (Williams, 1988). When the electromagnetic wave at w and the bound harmonic wave at 2w which is induced by the nonlinear polarization propagate through the medium, their amplitudes can change periodically depending on the phase relationship existing between them (Williams, 1988). The nonlinear interaction ends when these two waves exit the medium (Williams, 1988). It is at this point the relative intensities of the fundamental and harmonic frequencies are determined (Williams, 1988). If the harmonic and fundamental wave travel at the same velocity in the medium, which is called phase matching, the build up of the harmonic field is at its maximum, that is it has a large amplitude (Williams, 1988).
The waveguides used are made up of thin films. These thin films are made by depositing the dielectric or semiconductor film onto a substrate (Tien, 1971). The advantage of waveguides are that beams confined to regions of the order of their own wavelength of light can achieve very large intensities at very low power levels (Tien, 1971; Williams, 1988). The confinement of the beam can only be accomplished if there is an alteration of the refractive index along the length of the substrate in the waveguide (Miller, 1972; Bowden, 1988; Zanger & Zanger, 1991). Only two materials can produce two frequency wave for phase-matching in a thin film and these are birefringent materials and high nonlinear coefficient materials such as GaAs (Anderson & Boyd, 1971; Giordmaine, 1964). The thickness of the thin film determines whether the light modes will be phase matched (Tien, 1971; William, 1988). A light mode is the spatial distribution of optical energy propagated in the z direction in the waveguide (Williams, 1988). In mathematical terms, a mode is a solution of the Maxwell's equation by the electromagnetic wave (Williams, 1988). The boundary conditions in the Maxwell's equations permit only discrete modes to occur (Williams, 1988).
GaAs is chosen to be the nonlinear material for the waveguide since it has a large c (2) and low absorption coefficient (Anderson & Boyd, 1971). However, the GaAs dielectric waveguide has a low value for damage threshold by lasers (Anderson & Boyd, 1971). Therefore, Anderson & Boyd (1971) suggested that the dielectric waveguide should use a substrate that was transparent at the pump and harmonic frequency, and which would act as a heat sink. They further went on to suggest that multiple layers of GaxAl1-xAsx deposited onto a GaAs substrate by liquid epitaxy may yield a suitable condition in which high laser powers may enter and thus increase efficiency. This suggestion was used but instead of GaxAl1-xAsx material, AlGaAs was utilized (Miller, 1972; Zanger & Zanger, 1991). Thus, the altering of the refractive index can be achieved by building a heterostructure of GaAs and AlGaAs (Zanger & Zanger, 1991; Miller, 1992). GaAs is a heavy doped material having a larger refractive index than AlGaAs and the epitaxally grown AlGaAs is a lightly doped material (Zanger & Zanger, 1991; Miller, 1972). If GaAs material has a refractive index, n1 and the AlGaAs has a refractive index n2 (Zanger & Zanger, 1991; Miller, 1972). Then a n2-n1-n2 layer may be formed where the GaAs is the active area which forms a light waveguide that acts like an optical fibre (Fig. 6) so light is confined to only this active region (Zanger & Zanger, 1991; Miller, 1972).
According to Tien (1971) the phase match condition can be varied by varying the refractive index of the liquid that the film is submerged in. Also, the nonlinear interaction can then occur together in both the substrate and the film, or by themselves. Tien (1971) thus showed the phase matched conditons occurs when
(b /k)(1)= (b /k)(2)
where the superscripts 1 and 2 denote the fundamental and the harmonic respectively
k = w / c, where w is the angular frequency of the light wave and c is the speed of light.
b is the phase constant.
(b /k) is also the ratio between the speed of light in vacuum to the speed of wave propagation in the waveguide (Tien, 1971).
Tien (1971) also gave some simple rules to observe if the thickness of the film, W, was plotted against (b /k) for the fundamental and the harmonic wave the crossing point of the curves is the phase-match condition. Then the rules follow that:
1) dW/d(b /k) for the fundamental and the harmonic are always positive and the W vs (b /k) curves of the fundamental can cross that of the harmonic only once or not at all.
2) In general, when the W vs (b /k) curves show that a(1) > W(2) near (b /k)= no, where no is the refractive index of the substrate, a phase matched condition can be obtained when n1(2) < n1(2). Similarly when W(1) < W(2) near (b /k) = 0, the phase match can be obtain only when n1(2) > n1(1).
According to Anderson & Boyd (1971) phase matching was fabricated in their GaAs dielectric waveguide when using waveguide dispersion to compensate for refractive-index dispersion. Diffractionless propagation may occur in the film for distances only limited by the absorption and scattering loses in the film (Williams, 1988).
Williams (1988) showed that in a waveguide, the conversion efficiency is given by
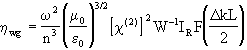
where h wg is the efficient of the waveguide
w is the angular frequency
m o and e o are the permeability and permittivity in free space respectively
c (2) is the second order susceptibility tensor
W is the waveguide thickness an overlap integral defined as
L is the interaction length
D k is the momentum difference at the fundamental and harmonic frequencies
F(D kL/2) is a phase mismatch factor defined as F(c ) = sin2 c /c 2 with c = D kL. The quantity D kL is a phase angle D f . F(c ) is zero at D k=0 and a maximum at p /2.
IR is the overlap integral defined as
![]()
where PNL is the nonlinear polarization
![]() is the harmonic field distribution
is the harmonic field distribution
s is the cross-sectional coordinate.
PNL is optimal at 1/W. In practical situations, the advantage of the waveguide is determined primarily by the coherence length (or degree of phase mismatch) within the waveguide (Williams, 1988).
These guides are used primarily to form and connect circuit elements in the integrated optics industry (Bowden, 1988).
GaAs is a very useful nonlinear material and thus can be used in many nonlinear applications particularly in the communications systems as can be seen in its use in a parametric amplifier and waveguides. However, recently there has been a move to replace nonlinear inorganic films like GaAs with polymers, since they have characteristics that may be useful in integrated optics. Therefore, the nonlinear characteristics of GaAs may have to be reapplied in other areas.
Anderson, D.B. & Boyd, J.T. (1971) "Wideband CO2 Laser Second Harmonic Generation Phase Matched in GaAs Thin Film Waveguides." Integrated Optics. IEEE Press Inc. Printed 1973. pp 261 - 263.
Brown, R. (1978) "Microwave Electronics." Vol. 10. The Encyclopedia Americana. Encyclopedia Americana Corporation. Internatinal Edition. pp.191
Bowden, M.J. (1988), "Polymers for Electronic and Photonic Applications." Advances in Chemistry Series 218: Electronic and Photonic applications of Polymers.
American Chemical Society, USA. pp. 50 -60.
Fischer, A.G. (1978) "Electroluminescence." Vol.10 The Encyclopedia Americana. Encyclopedia Americana Corporation. International Edition. pp. 153 -154.
Giordmaine, J.A. (1964), "The Interaction of Light with Light." Lasers and Light, Scientific American Inc. USA. Printed 1969. pp. 291 -302.
Hemenway, S.L.; Henry, R.W. & Caulton, C. (1967), "Physical Electronics." 2nd Edition. John Wiley and Sons, Inc. USA. pp.287.
Hyde, F.J. (1965), "Semiconductor." Macdonald and Co. (Publishers) Ltd., Great Britain. pp 191- 193.
Lindsay, R.B. (1978) "Electromagnetic Radiation". Vol.10. The Encyclopedia Americana. Encyclopedia Amerciana Corporation. International Edition. pp.160.
Miller, S.E. (1972) "A Survey of Integrated Optics". Integrated Optics. IEEE Press Inc. Printed 1973. USA. pp. 5 - 11.
Parker, S.P. (Editor), (1989), "Dictionary of scientific and technical terms." 4th Edition. McGraw Hill Inc. USA.
Roberts, G. G. (1988), "Molecular Electronics using Langmuir-Blodgett films." Advances in Chemistry Series 218: Electronic and Photonic Applications of Polymers. American Chemical Society, USA. pp 248.
Schawlow, A.L. (1969), " Properties and Applications of Laser Light." Lasers and Light . Scientific American Inc. Printed 1969. pp. 279.
Tien, P.K. (1971) "Light waves in Thin Films and Integrated Optics." Integrated Optics. IEEE Press Inc. Printed 1973. USA. pp 12 - 30.
Williams, D. (1988) "Polymers in Nonlinear Optics." Advances in Chemistry Series 218: Electronic and Photonic Applications of Polymers. American Chemical Society, USA. pp. 297 - 328.
Zanger, H. & Zanger C. (1991), "Fiber optics." Macmillan Publishing Company. USA. pp.191- 193